If I ask what are (3,4,5) or (5,12,13) or (15,8,17), most of us will answer that they are Pythagorean triplets. But you will be surprised to know that Pythagorean theorem was discovered during 570 – 500 BCE whereas some books on Vedic mathematics written during the period of 600 – 500 BCE has mentioned this theorem as SULBA SUTRA, which literally means ‘rule of chord’. SULBA SUTRA is a series of nine texts on the geometry of altar construction, dealing with rectangle, right sided triangles, rhombus etc. Sulba Sutra was introduced by Apastamba , Baudhayana , Manava , Katyayana and some others. Among them, Apastamba or Apastamba dharmasutra and Baudhayana are group of Sanskrit texts. Manava was the author of Hindu geometry text and Katyanana was a Sanskrit grammarian, mathematician and a Vedic priest lived in the ancient India.
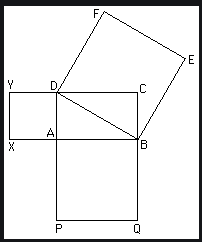
Katyayana belonged to the Aindra school of grammarians and might have lived towards the northwest of the Indian subcontinent. Katyayana Sulba Sutra consist of 6 chapters with 101 sutras and 7 chapters with 39 verses. Here he has given the solution of rational triangles and states the Pythagorean theorem in a generalized form. According to his Sanskrit shloka “the area of the square drawn on the diagonal (considering it as one of the sides) of a rectangle is equal to the sum of the areas of the square drawn separately on its breadth (considering it as one of the sides) and on its length(considering it as one of the sides).”
Katyayana Sulba Sutra also gives a geometric method to construct isosceles triangle equal in area to a given square and a geometric method to draw the perpendicular bisector of a given line. According to his Sanskrit verse the process to draw the perpendicular bisector of a given line is “after doubling (a given) cord, two loops (made at its two ends) are fixed at the two poles (of the Praci), and the cord is streched towards south by its middle point where a pole is fixed ; the same is repeated to the north. This line joining the two poles is the north-south line (Udici).”
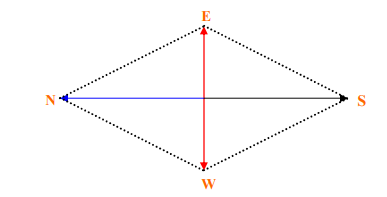
They used to use all these geometric methods to construct the fire altar during their prayers.
Author:
Samprity Das
M.Sc in Applied mathematics
Areas of Research Interest:
Operational Research,
Application of Differential Calculus and Differential Equations to Physical and Biological Systems
Research Associate
Academy of Research for Cultivation of Indian Science
Email: Sampritydas19@gmail.com
